Numpy and Matplotlib¶
These are two of the most fundamental parts of the scientific python "ecosystem". Most everything else is built on top of them.
In [1]:
import numpy as np
What did we just do? We imported a package. This brings new variables (mostly functions) into our interpreter. We access them as follows.
In [2]:
# find out what is in our namespace
dir()
Out[2]:
In [3]:
# find out what's in numpy
dir(np)
Out[3]:
In [4]:
# find out what version we have
np.__version__
Out[4]:
The numpy documentation is crucial!
http://docs.scipy.org/doc/numpy/reference/
NDArrays¶
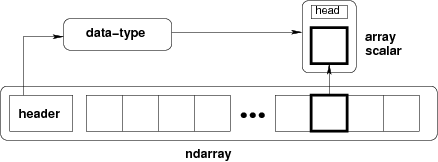
The core class is the numpy ndarray (n-dimensional array).
In [5]:
from IPython.display import Image
Image(url='http://docs.scipy.org/doc/numpy/_images/threefundamental.png')
Out[5]:
In [6]:
# create an array from a list
a = np.array([9,0,2,1,0])
In [7]:
# find out the datatype
a.dtype
Out[7]:
In [8]:
# find out the shape
a.shape
Out[8]:
In [9]:
# what is the shape
type(a.shape)
Out[9]:
In [10]:
# another array with a different datatype and shape
b = np.array([[5,3,1,9],[9,2,3,0]], dtype=np.float64)
In [11]:
# check dtype and shape
b.dtype, b.shape
Out[11]:
Important Concept: The fastest varying dimension is the last dimension! The outer level of the hierarchy is the first dimension. (This is called "c-style" indexing)
More array creation¶
There are lots of ways to create arrays.
In [12]:
# create some uniform arrays
c = np.zeros((9,9))
d = np.ones((3,6,3), dtype=np.complex128)
e = np.full((3,3), np.pi)
e = np.ones_like(c)
f = np.zeros_like(d)
In [13]:
# create some ranges
np.arange(10)
Out[13]:
In [14]:
# arange is left inclusive, right exclusive
np.arange(2,4,0.25)
Out[14]:
In [15]:
# linearly spaced
np.linspace(2,4,20)
Out[15]:
In [16]:
# log spaced
np.logspace(1,2,10)
Out[16]:
In [17]:
# two dimensional grids
x = np.linspace(-2*np.pi, 2*np.pi, 100)
y = np.linspace(-np.pi, np.pi, 50)
xx, yy = np.meshgrid(x, y)
xx.shape, yy.shape
Out[17]:
Indexing¶
Basic indexing is similar to lists
In [18]:
# get some individual elements of xx
xx[0,0], xx[-1,-1], xx[3,-5]
Out[18]:
In [19]:
# get some whole rows and columns
xx[0].shape, xx[:,-1].shape
Out[19]:
In [20]:
# get some ranges
xx[3:10,30:40].shape
Out[20]:
There are many advanced ways to index arrays. You can read about them in the manual. Here is one example.
In [21]:
# use a boolean array as an index
idx = xx<0
yy[idx].shape
Out[21]:
In [22]:
# the array got flattened
xx.ravel().shape
Out[22]:
In [23]:
f = np.sin(xx) * np.cos(0.5*yy)
At this point you might be getting curious what these arrays "look" like. So we need to introduce some visualization.
In [24]:
from matplotlib import pyplot as plt
%matplotlib inline
In [25]:
plt.pcolormesh(f)
Out[25]:
Manipulating array dimensions¶
In [26]:
# transpose
plt.pcolormesh(f.T)
Out[26]:
In [27]:
# reshape an array (wrong size)
g = np.reshape(f, (8,9))
In [28]:
# reshape an array (right size) and mess it up
print(f.size)
g = np.reshape(f, (200,25))
plt.pcolormesh(g)
Out[28]:
In [29]:
# tile an array
plt.pcolormesh(np.tile(f,(6,1)))
Out[29]:
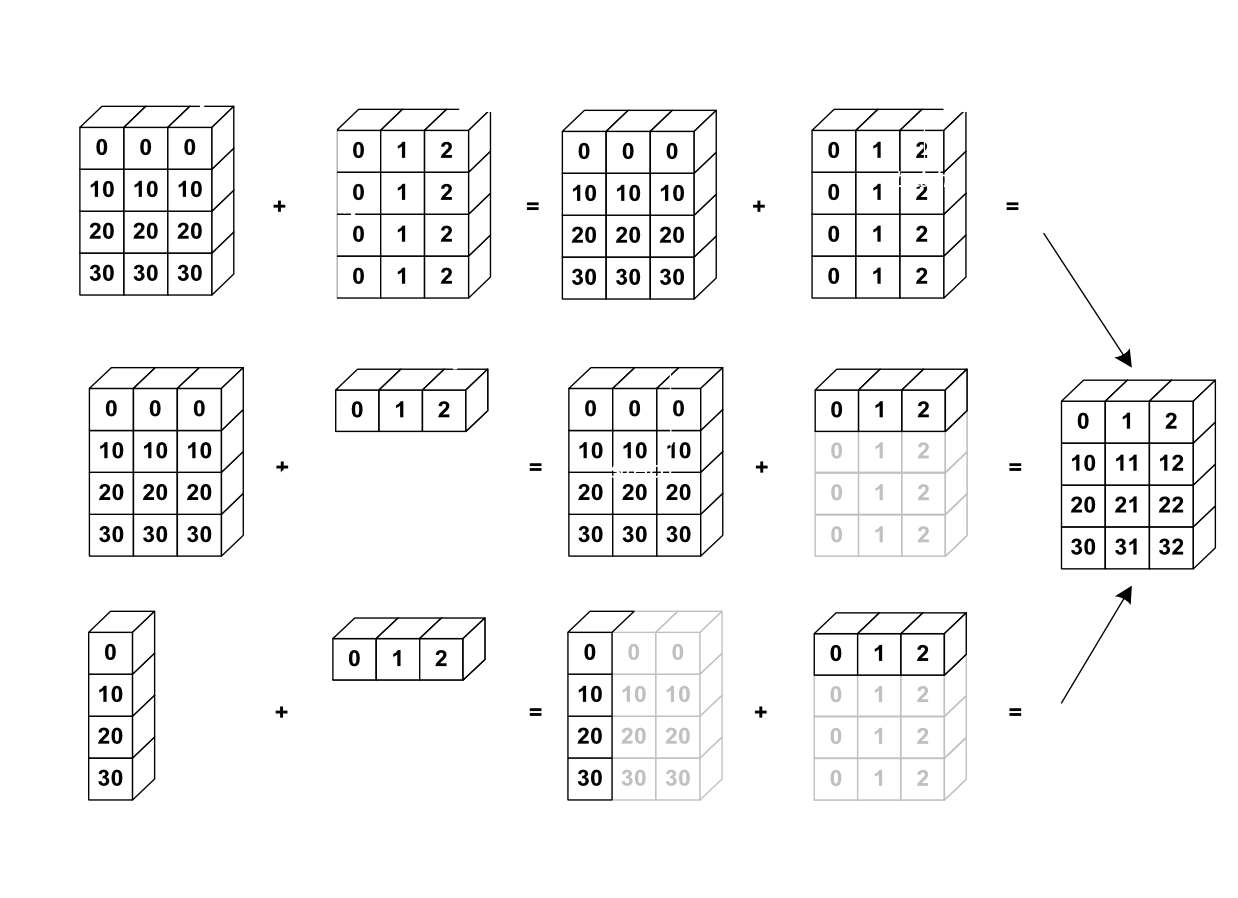
Broadcasting¶
Broadcasting is an efficient way to multiply arrays of different sizes
In [30]:
Image(url='http://scipy-lectures.github.io/_images/numpy_broadcasting.png',
width=720)
Out[30]:
In [31]:
# multiply f by x
print(f.shape, x.shape)
g = f * x
print(g.shape)
In [32]:
# multiply f by y
print(f.shape, y.shape)
h = f * y
print(h.shape)
In [33]:
# use newaxis special syntax
h = f * y[:,np.newaxis]
print(h.shape)
In [34]:
plt.pcolormesh(g)
Out[34]:
Reduction Operations¶
In [35]:
# sum
g.sum()
Out[35]:
In [36]:
# mean
g.mean()
Out[36]:
In [37]:
# std
g.std()
Out[37]:
In [38]:
# apply on just one axis
g_ymean = g.mean(axis=0)
g_xmean = g.mean(axis=1)
In [39]:
plt.plot(x, g_ymean)
Out[39]:
In [40]:
plt.plot(g_xmean, y)
Out[40]:
Fancy Plotting¶
Enough lessons, let's have some fun.
In [41]:
fig = plt.figure(figsize=(12,8))
ax1 = plt.subplot2grid((6,6),(0,1),colspan=5)
ax2 = plt.subplot2grid((6,6),(1,0),rowspan=5)
In [42]:
fig = plt.figure(figsize=(10,6))
ax1 = plt.subplot2grid((6,6),(0,1),colspan=5)
ax2 = plt.subplot2grid((6,6),(1,0),rowspan=5)
ax3 = plt.subplot2grid((6,6),(1,1),rowspan=5, colspan=5)
ax1.plot(x, g_ymean)
ax2.plot(g_xmean, y)
ax3.pcolormesh(x, y, g)
ax1.set_xlim([x.min(), x.max()])
ax3.set_xlim([x.min(), x.max()])
ax2.set_ylim([y.min(), y.max()])
ax3.set_ylim([y.min(), y.max()])
plt.tight_layout()
Real Data¶
ARGO float profile from North Atlantic
In [45]:
# download with curl
!curl -O https://www.ldeo.columbia.edu/~rpa/argo_float_4901412.npz
In [46]:
# load numpy file and examine keys
data = np.load('argo_float_4901412.npz')
data.keys()
Out[46]:
In [47]:
# access some data
T = data['T']
In [48]:
# there are "nans", missing data, which screw up our routines
T.min()
Out[48]:
In [49]:
ar_w_mask = np.ma.masked_array([1, 2, 3, 4, 5],
mask=[True, True, False, False, False])
ar_w_mask
Out[49]:
In [50]:
ar_w_mask.mean()
Out[50]:
In [51]:
T_ma = np.ma.masked_invalid(T)
T_ma.mean()
Out[51]:
Masked Arrays¶
This is how we deal with missing data in numpy
In [52]:
# create masked array
T = np.ma.masked_invalid(data['T'])
type(T)
Out[52]:
In [53]:
# max and min
T.max(), T.min()
Out[53]:
In [54]:
# load other data
S = np.ma.masked_invalid(data['S'])
P = np.ma.masked_invalid(data['P'])
In [55]:
# scatter plot
plt.scatter(S, T, c=P)
plt.grid()
plt.colorbar()
Out[55]:
In [ ]:
In [ ]: